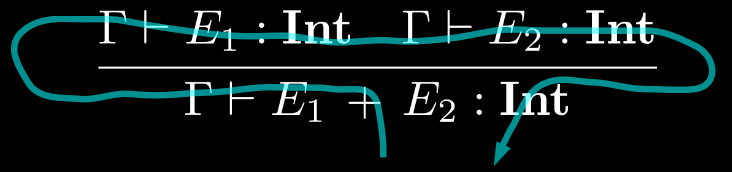Type Analysis

A type is a collection of values (integers, strings, functions, trees, images, etc)

A type is a way to interpret a sequence of bits

A type is a computable property of programs that garuntees some property of their execution

A type system is a set of rules that define a typing relation

A typing relation is a set of triples denoted , where:

• is the typing context, which is the symbol table that maps each identifier to its meaning
• is the term corresponding to a subtree of the parse tree
• is the type

and we traditionally write to mean .

An inference rule is a collection of zero or more premises and a conclusion.

The premises are written above a horizontal line and the conclusion below the line. The rule asserts that if the premises hold, then the conclusion holds, just like in formal logic!

Please add this new tuple to the set
- Prof. Ondřej Lhoták

A well-formedness relation is a set of pairs denoted , where:

• is the parsing context (symbol table)
• is a term (parse tree)

and we traditionally write to mean .

this means a numeric literal will always have the type integer.

this means, if we use a variable that is in the symbol table with name ID of type , then we add it to the symbol table.

if we tried something goofy ahh like main + main (where main is a procedure), then we would have an error, because there is no rule that takes two functions and adds them together.

A more intuitive way of looking at this is, if and , then the triple containing the tree corresponding to the expression . This is because when we have an arithmetic expression, every expression in the tree must evaluate to an integer.

For example, if we tried something even more goofy, like 5 * 2 + (3 * main), then we have an error, because ONE of the expression subtrees is invalid.

When we write (1 + 3) * (2 + 5), note that , etc.

in LACS, assignment "returns" its value as an expression (like in Javascript).

means any type (we don't care what type, since it won't be in the rule), but it MUST be SOME type

When we have a block expression, the last thing that shows up is the type that the block evaluates to (in LACS, we must use semicolons). In this way, if we have a function like def func() = {a = 5; 3}, our block {a = 4; 3} evaluates to type Int, regardless of what came before it.

this means if we have a procedure with params , then we can call it with the correct parameters (whether they are literals or variables). Note that the second parameter is saying that for every parameter, the types of some value matches the types of the param list.

this rule defines the well-formedness of the root node of the parse tree, which is expanded using production rule defdefs -> defdef defdefs or defdefs -> defdef.
The premise is checking that every procedure is well-formed (checked by the next rule)
The conclusion adds the list of top-level function declarations with an empty symbol table to the set. We can do this because in LACS, there are no global variables.

• What everything means:
  • : procedure params
  • : local variable declarations
  • : nested procedures
• The first premise enforces the requirement that parameters, variables, and nested procedure declarations must hav distinct names
• The second premise states that the symbol table is extended with the declarations of the parameters, variable declarations, and nested procedure declarations, and that each nested procedure declaration must be recursively well-formed using this extended symbol table
  • The commas mean that any new declarations take precedence over (replace) declarations of the same name in . That is, we take the "nearest" (innermost) scope of declaration for a name
• The third premise states that the body of the procedure may refer to any of the parameters, variables, and nested procedures declared in that procedure, as well as those declared in any outer enclosing scopes
  • Note that this premise is a type-checking premise, not a well-formed premise
  • We are type-checking with our new extended symbol table
  • In order for a procedure declaration to be well-formed, the body must have a type according to the typing rules
    • I.e
  • The rule also checks that the return type is correct
• Note that in LACS, you must declare in order: local variables, nested procedures, expressions
• This rule corresponds to the grammar rule defdef -> DEF ID LPAREN parmsopt RPAREN COLON type BECOMES LBRACE vardefsopt defdefsopt expras RBRACE

A type system is sound if when it assigns a type to an expression, the expression evaluates to a value of the same type

The triple only if the conclusion of some inference rule put it there

Therefore, the implementation of the type checker can look at the grammar production rule in the root node of the tree and implement the inference rule corresponding to that production rule.

With values for the metavariables, the type checker checks the premises of the inference rule. In many cases, this involves recursive calls to determine types for subtrees of .

The property that the syntactic form of each parse tree node determines which inference rule to apply and suggests values for metavariables in the rule is specific to LACS. Other type systems may require more complex algorithms to search for ways to apply inference rules and instantiate metavariables to find a triple

For each inference rule, start with the bottom left (syntactic shape of the tree) to the top (to check the premises) to the bottom right (return the type)