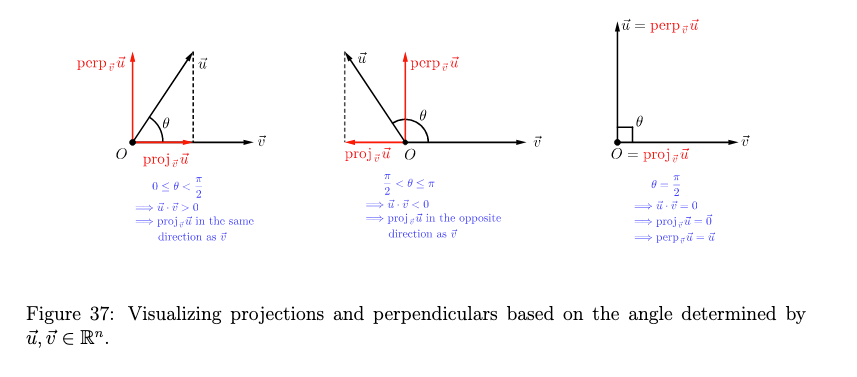
Midterm Review

Properties

(if and only if)
!!!
!!! for
!!!
(modulus)

!!! Denotes a non-trivial point

Properties

Powers of Complex Numbers

DeMoivre's Theorem (DMT)

Theorem

The exponent of a complex number in polar form is:

For and any

Proof

For the integer , we either have or .

Case 1: , proof by induction

Let be the open sentence

Base case: For , the statement is
LS =
RS =

is true

Inductive step
Let be an arbitrary integer, where
Assume the inductive hypothesis,
We wish to prove

So the result is true for , and hence holds true for all by POMI.

Case 2: . Let

(See Pythagorean identities, Symmetry)

Complex nth Roots Theorem (CNRT)

Theorem

The th root of a complex number in polar form is:

For , , , and .
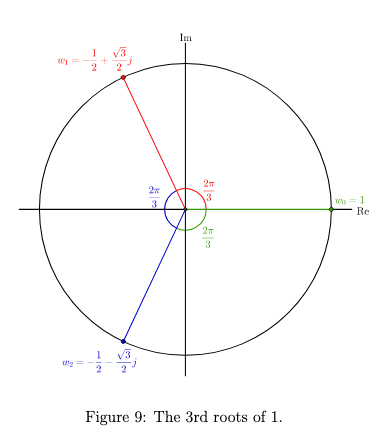
Complex 3rd Roots of 1.png

Remark

These roots will form an n-regular polygon

Proof

Let be an arbitrary complex number, and be an arbitrary natural numbers. We define the two sets:

(See Set Builder Notation)

We will prove that by proving that and (see set equality)

Forward direction: : we prove the implication (see proving subsets)
Let be an arbitrary integer in , and assume that

Then, using DeMoivre's Theorem, we obtain

(See periodicity)

Thus we conclude that

Backward direction: : we prove the implication
Assume that < so , and suppose that has polar form .
Then, writing the equation in polar form, we have

where we have used DMT on the left side.
How, two complex numbers in polar form are equal if and only if their moduli are equal, and their arguments differ by an integer multiple of .
Thus, from the equation above we obtain , and for some , meaning

Hence, for some < we have

Now, dividing by , the division algorithm gives

for some and .

Substituting into equation (1) gives

We conclude that

Powers of Complex Numbers

DeMoivre's Theorem (DMT)

Theorem

The exponent of a complex number in polar form is:

For and any

Proof

For the integer , we either have or .

Case 1: , proof by induction

Let be the open sentence

Base case: For , the statement is
LS =
RS =

is true

Inductive step
Let be an arbitrary integer, where
Assume the inductive hypothesis,
We wish to prove

So the result is true for , and hence holds true for all by POMI.

Case 2: . Let

(See Pythagorean identities, Symmetry)

Complex nth Roots Theorem (CNRT)

Theorem

The th root of a complex number in polar form is:

For , , , and .
Complex 3rd Roots of 1.png

Remark

These roots will form an n-regular polygon

Proof

Let be an arbitrary complex number, and be an arbitrary natural numbers. We define the two sets:

(See Set Builder Notation)

We will prove that by proving that and (see set equality)

Forward direction: : we prove the implication (see proving subsets)
Let be an arbitrary integer in , and assume that

Then, using DeMoivre's Theorem, we obtain

(See periodicity)

Thus we conclude that

Backward direction: : we prove the implication
Assume that < so , and suppose that has polar form .
Then, writing the equation in polar form, we have

where we have used DMT on the left side.
How, two complex numbers in polar form are equal if and only if their moduli are equal, and their arguments differ by an integer multiple of .
Thus, from the equation above we obtain , and for some , meaning

Hence, for some < we have

Now, dividing by , the division algorithm gives

for some and .

Substituting into equation (1) gives

We conclude that

Euler's Formula

Definition

For , where the right side is a complex number in polar form

We can sorta prove this with a Taylor Series:

Example - Euler's Formula

Euler and complex numbers:

Euler noticed that this follows the same pattern as the derivatives of sine/cosine (i.e as you take more derivatives, it "cycles" through).

which is Euler's Formula!

Note that we got the values for and from the two examples above.

Complex Exponential Form

Definition

Since the complex exponential form is not unique,

Euler's Identity

Identity

Consider Euler's Formula with , . It follows that

Properties

if and only if. zero vector
(Triangle inequality)

Unit Vector

Definition

Given vector of :

Note that is parallel to , but is a unit vector, so

Properties

Cauchy-Schwarz Inequality

Definition

Complex Inner Product

Definition

Note that in non-engineering math, the conjugate is placed on the second variable

It follows that the definition of the magnitude for complex vectors is also different:

Also

Properties

Let and . Then:

Complex Inner Product

Definition

Note that in non-engineering math, the conjugate is placed on the second variable

It follows that the definition of the magnitude for complex vectors is also different:

Also

Properties

Let and . Then:

Cross Product

Definition - 3-space

Only defined in 3-space, produces a vector perpendicular to and

Given and , then

Definition

So

(see standard basis, Determinants)

Intuition

Recall that the determinant is the area of a parallelogram. That means the cross-product is also the area of a parallelogram (see below).

Theorem

For any 2 non-zero vectors in 3-space, if , then and are colinear

Properties

Application - Area of a Parallelogram

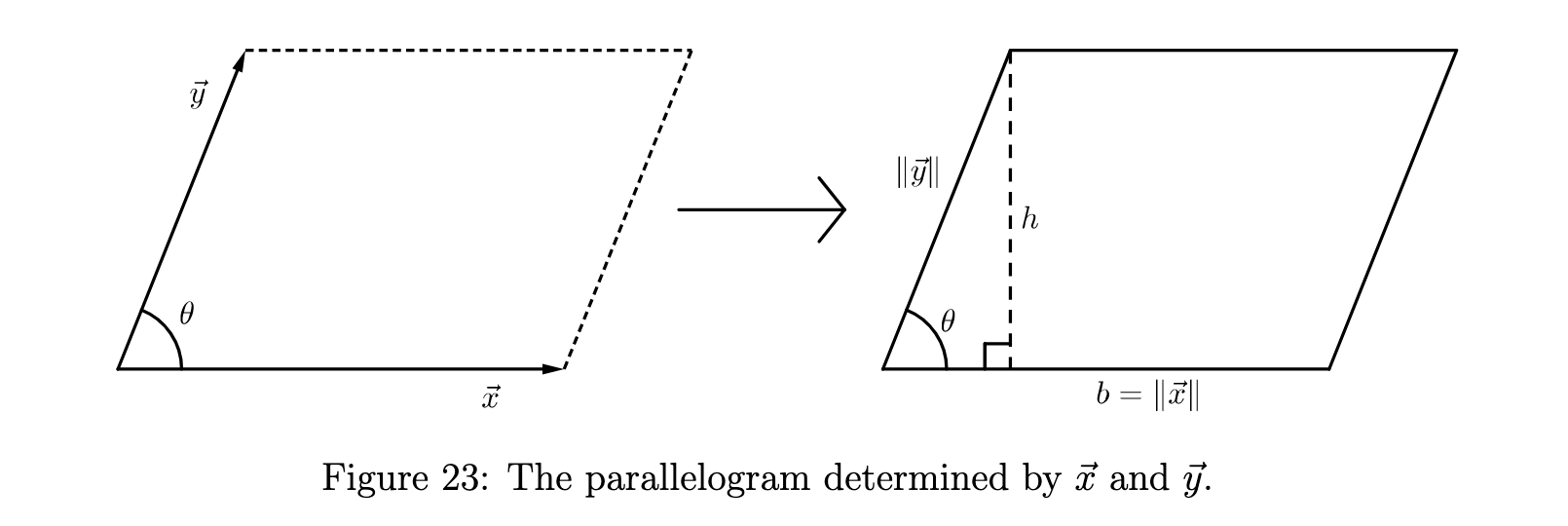
Area of a Parallelogram.png
We see that and satisfies , which gives

And the area of a triangle is calculated as half the area of a paralellogram

Volume of a Parallelepiped:
Dot product the cross product VECTOR

Hand Rule

Figure

The resulting direction of :

The left hand rule is more "intuitive" as the first vector is the bottom finger, while the right hand needs to mimic the left hand by swapping fingers.

Lagrange Identity

Identity

Where

Cross Product Order

Definition

In Cartesian coordinates:

In Cylindrical Coordinates:

In Spherical Coordinates:

What this means:

The same applies to the rest of the coordinate systems.

Projection

Definition

The projection of onto :

Definition

The projection of perpendicular po :

Midterm Review

Properties of Conjugates

Properties of Modulus

Powers of Complex Numbers

DeMoivre's Theorem (DMT)

Complex nth Roots Theorem (CNRT)

Powers of Complex Numbers

DeMoivre's Theorem (DMT)

Complex nth Roots Theorem (CNRT)

Euler's Formula

Complex Exponential Form

Euler's Identity

Properties of Norms

Unit Vector

Properties of Dot Products

Cauchy-Schwarz Inequality

Complex Inner Product

Complex Inner Product

Cross Product

Hand Rule

Lagrange Identity

Cross Product Order

Projection