Fundamental Theorem of Calculus

The Connection Between Integral and Differential Calculus

Consider a function , continuous and positive on the interval . Let be the area below the curve between and another arbitrary point in .

If we add a thin strip to the right of width , we find that the area of the strip must be .

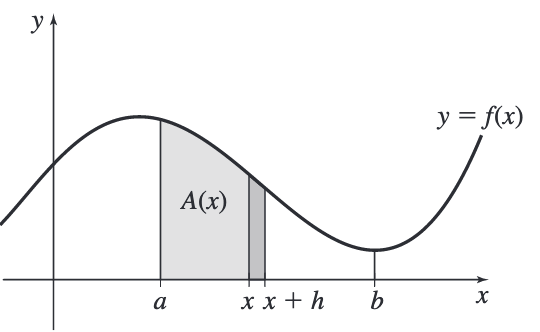
Since it's nearly rectangular, the area is approximately .

For small values of , we have

So

So the derivative of the area under the graph is equal to the original function.

Fundamental Theorem of Calculus, Part 1 (FTC 1)

Or, more concisely

So we call the antiderivative of

Constant of Integration

Since constants differentiate to 0, there are infinitely many antiderivatives.

Fundamental Theorem of Calculus, Part 2 (FTC 2)