Powers and Roots of Complex Numbers

Powers of Complex Numbers

DeMoivre's Theorem (DMT)

Theorem

The exponent of a complex number in polar form is:

For and any

Proof

For the integer , we either have or .

Case 1: , proof by induction

Let be the open sentence

Base case: For , the statement is
LS =
RS =

is true

Inductive step
Let be an arbitrary integer, where
Assume the inductive hypothesis,
We wish to prove

So the result is true for , and hence holds true for all by POMI.

Case 2: . Let

(See Pythagorean identities, Symmetry)

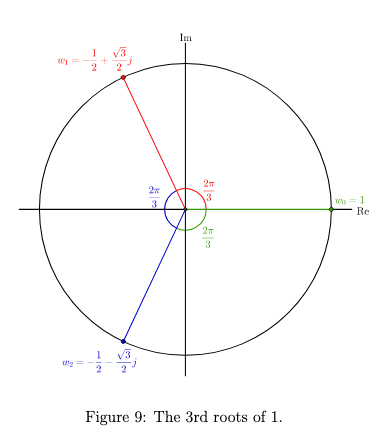
Complex nth Roots Theorem (CNRT)

Theorem

The th root of a complex number in polar form is:

For , , , and .
Complex 3rd Roots of 1.png

Remark

These roots will form an n-regular polygon

Proof

Let be an arbitrary complex number, and be an arbitrary natural numbers. We define the two sets:

(See Set Builder Notation)

We will prove that by proving that and (see set equality)

Forward direction: : we prove the implication (see proving subsets)
Let be an arbitrary integer in , and assume that

Then, using DeMoivre's Theorem, we obtain

(See periodicity)

Thus we conclude that

Backward direction: : we prove the implication
Assume that < so , and suppose that has polar form .
Then, writing the equation in polar form, we have

where we have used DMT on the left side.
How, two complex numbers in polar form are equal if and only if their moduli are equal, and their arguments differ by an integer multiple of .
Thus, from the equation above we obtain , and for some , meaning

Hence, for some < we have

Now, dividing by , the division algorithm gives

for some and .

Substituting into equation (1) gives

We conclude that