Functions

Definition

A function is a rule that assigns to every element in one set (the domain), a unique element to another set (the codomain), and the resulting mapped set is the range.

Where the codomain is the set of all possible outputs of the function, the range it the set that actually comes out.

Given sets and , we write to indicate that is a function with domain and codomain , and it is understood that each element , and the function assigns a unique element .

We say that maps to , and that is the image of under . We typically write .

Formally, a function is a binary relation that is functional and total.

Partial, or non-total functions do exist, but generally "function" is taken mean a total function. That is, it maps every value on its assigned domain to its value. You may have functions with hole or discontinuities, but when defining their domains, those missing bits are omitted, so they are still total functions.

Example

For example, the function , the codomain is , but the range is (see set builder notation, rational function).

Diagram

Injective, Surjective, Bijective

Diagram

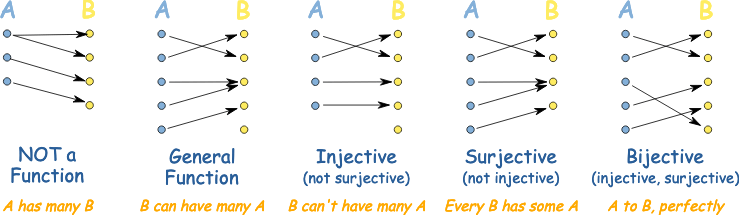
Injective

A function is injective if: .

That is, is mapped to by no more than 1 .

(see quantified statement, Implications)

More formally, a function is injective iff it is an injective relation.

Example

The function:

is not injective, because:

Surjective

A function is surjective if:

That is, every is mapped to by some .

More formally, a function is surjective iff it is an surjective relation.

Example

is surjective when the range , but it is not surjective for the codomain

Example

given by is surjective. But if it becomes given by , then it is no longer surjective.

Bijective

is bijective if it is both injective and surjective. That is, every maps to a a different , and every has a mapping by .